一农民带上若干千克自产的土豆进城出售，为了方便，他带了一些零钱备用，按市场价售出一些后，又降价出售，售出的土豆千克数与他手中持有的钱数（含备用零钱）的关系，如图所示，结合图象回答下列问题．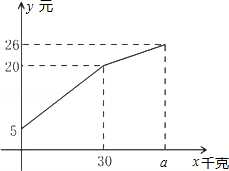
（1）农民自带的零钱是多少？
（2）试求降价前y与x之间的关系式？
（3）由表达式你能求出降价前每千克的土豆价格是多少？
（4）降价后他按每千克0.4元将剩余土豆售完，这时他手中的钱（含备用零钱）是26元，试问他一共带了多少千克土豆？
相关试题
，tanB=
，求BD的长．
一袋装有编号为1，2，3的三个形状、大小、材质等相同的小球，从袋中随意摸出1个球，记事件A为“摸出的球编号为奇数”，随意抛掷一个质地均匀正方体骰子，六个面上分别写有1-6这6个整数，记事件B为“向上一面的数字是3的整数倍”，请你判断等式“P（A）=2P（B）”是否成立，并说明理由．
，其中x=2．
相关知识点
推荐套卷
粤公网安备 44130202000953号