如图1,△ABC中,∠BAC=90°,AB=AC,AD⊥BC于点D,点E在AC边上,连结BE.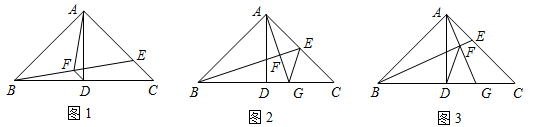
(1)若AF是△ABE的中线,且AF=5,AE=6,连结DF,求DF的长;
(2)若AF是△ABE的高,延长AF交BC于点G.
①如图2,若点E是AC边的中点,连结EG,求证:AG+EG=BE;
②如图3,若点E是AC边上的动点,连结DF.当点E在AC边上(不含端点)运动时,∠DFG的大小是否改变,如果不变,请求出∠DFG的度数;如果要变,请说明理由.
相关知识点
推荐套卷
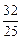 的k值?若存在,请求出符合的k值;若不存在,请说明理由。
的k值?若存在,请求出符合的k值;若不存在,请说明理由。 的汽车拥有量已达72万辆.
的汽车拥有量已达72万辆. 1)求证:△ABD为等腰三角形;
1)求证:△ABD为等腰三角形;
 粤公网安备 44130202000953号
粤公网安备 44130202000953号