《中国足球改革总体方案》提出足球要进校园．为了解某校学生对校园足球喜爱的情况，随机对该校部分学生进行了调查，将调查结果分为“很喜欢”、“较喜欢”、“一般”、“不喜欢”四个等级，并根据调查结果绘制成了如下两幅不完整的统计图：
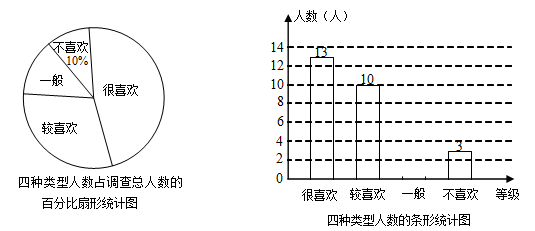
（1）一共调查了 名学生，请补全条形统计图；
（2）在此次调查活动中，选择“一般”的学生中只有两人来自初三年级．现在要从选择“一般”的同学中随机抽选两人来谈谈各自对校园足球的感想，请用画树状图或列表法求选中的两人刚好都来自初三年级的概率．
相关试题
如图，已知A（－4，2）、B（2，－4）是一次函数y＝kx＋b的图象和反比例函数y＝ 
的图象上的两个交点．
（1）求反比例函数和一次函数的解析式；
（2）求直线AB与y轴的交点C的坐标及△AOB的面积；
如图所示，在梯形ABCD中，AB∥CD，DB平分∠ADC，过点A作AE∥BD，交CD的延长线于点E，且∠C=2∠E．
（1）求证：梯形ABCD是等腰梯形．
（2）若∠BDC=30°，AD=5，求CD的长．
如图所示，已知点D在△ABC的边BC上，DE∥AC，交AB于点E，DF∥AB，交AC于点F．
（1）求证：AE=DF
（2）若AD平分∠BAC，试判断四边形AEDF的形状，并说明理由．
相关知识点
推荐套卷
粤公网安备 44130202000953号