如图，在平面直角坐标系中，直线y=0．5x+2与x轴、y轴分别交于A、B两点，以AB为边在第二象限内作正方形ABCD，过点D作DE⊥x轴，垂足为E．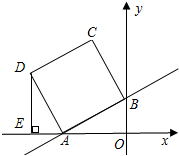
（1）求点A、B的坐标，并求边AB的长；
（2）求点D的坐标；
（3）你能否在x轴上找一点M，使△MDB的周长最小？如果能，请求出M点的坐标；如果不能，说明理由．
相关试题
，其中
满足
；
，其中
，小马在计算
时，由于粗心把
求得结果为
，请你帮小马算出
；（2）
（2）
（4）
相关知识点
推荐套卷
如图，在平面直角坐标系中，直线y=0．5x+2与x轴、y轴分别交于A、B两点，以AB为边在第二象限内作正方形ABCD，过点D作DE⊥x轴，垂足为E．
（1）求点A、B的坐标，并求边AB的长；
（2）求点D的坐标；
（3）你能否在x轴上找一点M，使△MDB的周长最小？如果能，请求出M点的坐标；如果不能，说明理由．
粤公网安备 44130202000953号