为了保护环境，某工厂在国家的号召下，把废弃物回收转化为某种产品，经测算，处理成本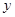
（万元）与处理量
（吨）之间的函数关系可近似的表示为：
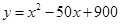，且每处理一吨废弃物可得价值为
万元的某种产品，同时获得国家补贴万元．当
时，判断该项举措能否获利？如果能获利，求出最大利润；如果不能获利，请求出国家最少补贴多少万元，该工厂才不会亏损？
3,求
的值; 
，且
．
在
上的单调性，并给予证明；
. 
的奇偶性；
，集合
．
时，
； (2) 若
，求实数
的取值范围．
和直线
的交点
的坐标，及点
的距离。推荐套卷
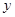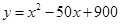为了保护环境，某工厂在国家的号召下，把废弃物回收转化为某种产品，经测算，处理成本（万元）与处理量（吨）之间的函数关系可近似的表示为：，且每处理一吨废弃物可得价值为万元的某种产品，同时获得国家补贴万元．当时，判断该项举措能否获利？如果能获利，求出最大利润；如果不能获利，请求出国家最少补贴多少万元，该工厂才不会亏损？
粤公网安备 44130202000953号