如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:
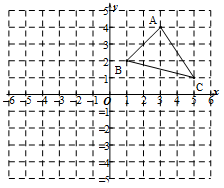
(1)△ABC的面积为
(2) 画出格点△ABC(顶点均在格点上)关于x轴对称的△
(3)指出△ 的顶点坐标.
的顶点坐标.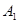 ( , ),
( , ), 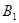 ( , ),
( , ), 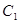 ( , )
( , )
(4)在y轴上画出点Q,使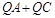 最小。
最小。
相关知识点
推荐套卷
如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:

(1)△ABC的面积为
(2) 画出格点△ABC(顶点均在格点上)关于x轴对称的△
(3)指出△ 的顶点坐标.
的顶点坐标.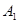 ( , ),
( , ), 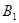 ( , ),
( , ), 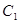 ( , )
( , )
(4)在y轴上画出点Q,使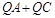 最小。
最小。