如某校初三（1）班50名学生需要参加体育“五选一”自选项目测试，班上学生所报自选项目的情况统计表如下：
（1）求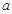
，
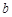的值；
（2）若将各自选项目的人数按所占比例绘制成扇形统计图，求“长跑”对应扇形的圆心角的度数；
（3）在选报“长跑”的学生中，有3名男生，2名女生，为了了解学生的训练效果，从这5名学生中随机抽取两名学生进行推铅球测试，用列表法或树形图法求出所抽取的两名学生中恰有一名女生的概率．
相关试题
中，
6，
8，
平分∠
交
于点
，
平分∠
交
于点
．
为平行四边形；
中，点
是
的中点，且
⊥
．
的度数；
的长；
为一梯形纸片，
∥
，
．翻折纸片
与点
重合，折痕为
．已知
⊥
.
中，
∥
，
，
⊥
，延长
至点
，使
．
的度数．
为等腰三角形．
中，
是
边上一点，
的延长线交
的延长线于点
，
⊥
，垂足为
，且
．
；推荐套卷
如某校初三（1）班50名学生需要参加体育“五选一”自选项目测试，班上学生所报自选项目的情况统计表如下：
（1）求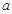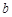，的值；
（2）若将各自选项目的人数按所占比例绘制成扇形统计图，求“长跑”对应扇形的圆心角的度数；
（3）在选报“长跑”的学生中，有3名男生，2名女生，为了了解学生的训练效果，从这5名学生中随机抽取两名学生进行推铅球测试，用列表法或树形图法求出所抽取的两名学生中恰有一名女生的概率．
粤公网安备 44130202000953号