已知定点F（3，0）和动点P（x，y），H为PF的中点，O为坐标原点，且满足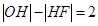
．
（1）求点P的轨迹方程；
（2）过点F作直线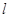
与点P的轨迹交于A，B两点，点C（2，0）．连接AC，BC与直线
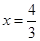分别交于点M，N．试证明：以MN为直径的圆恒过点F．
,且
，求证：
.
在
处取得极值－2.
的解析式； 
在点
处的切线方程.
求证：
.
的单调区间;
上的最小值;
,
恒成立,求实数
的取值范围．推荐套卷
已知定点F（3，0）和动点P（x，y），H为PF的中点，O为坐标原点，且满足．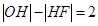
（1）求点P的轨迹方程；
（2）过点F作直线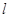与点P的轨迹交于A，B两点，点C（2，0）．连接AC，BC与直线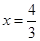分别交于点M，N．试证明：以MN为直径的圆恒过点F．
粤公网安备 44130202000953号