设某物体一天中的温度T是时间t的函数,已知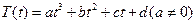 ,其中温度的单位是℃,时间的单位是小时.中午12:00相应的t=0,中午12:00以后相应的t取正数,中午12:00以前相应的t取负数(如早上8:00相应的t=-4,下午16:00相应的t=4).若测得该物体在早上8:00的温度为8℃,中午12:00的温度为60℃,下午13:00的温度为58℃,且已知该物体的温度早上8:00与下午16:00有相同的变化率.
,其中温度的单位是℃,时间的单位是小时.中午12:00相应的t=0,中午12:00以后相应的t取正数,中午12:00以前相应的t取负数(如早上8:00相应的t=-4,下午16:00相应的t=4).若测得该物体在早上8:00的温度为8℃,中午12:00的温度为60℃,下午13:00的温度为58℃,且已知该物体的温度早上8:00与下午16:00有相同的变化率.
(1)求该物体的温度T关于时间t的函数关系式;
(2)该物体在上午10:00到下午14:00这段时间中(包括端点)何时温度最高?最高温度是多少?