如图,已知抛物线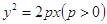 上点
上点 到焦点
到焦点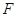 的距离为3,直线
的距离为3,直线 交抛物线
交抛物线 于
于 两点,且满足
两点,且满足 。圆
。圆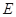 是以
是以 为圆心,
为圆心, 为直径的圆。
为直径的圆。
(1)求抛物线 和圆
和圆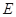 的方程;
的方程;
(2)设点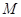 为圆
为圆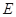 上的任意一动点,求当动点
上的任意一动点,求当动点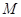 到直线
到直线 的距离最大时的直线方程。
的距离最大时的直线方程。
相关知识点
推荐套卷
如图,已知抛物线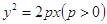 上点
上点 到焦点
到焦点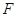 的距离为3,直线
的距离为3,直线 交抛物线
交抛物线 于
于 两点,且满足
两点,且满足 。圆
。圆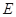 是以
是以 为圆心,
为圆心, 为直径的圆。
为直径的圆。
(1)求抛物线 和圆
和圆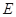 的方程;
的方程;
(2)设点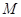 为圆
为圆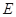 上的任意一动点,求当动点
上的任意一动点,求当动点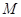 到直线
到直线 的距离最大时的直线方程。
的距离最大时的直线方程。