甲、乙两人共同抛掷一枚硬币，规定硬币正面朝上甲得1分，否则乙得1分，先积得3分者获胜，并结束游戏．
（Ⅰ）求在前3次抛掷中甲得2分，乙得1分的概率；
（Ⅱ）若甲已经积得2分，乙已经积得1分，求甲最终获胜的概率；
（Ⅲ）用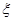
表示决出胜负抛硬币的次数，求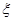的分布列及数学期望．
相关试题
与
轴两交点
．
为直径的圆
的方程；
的顶点在圆
应满足什么条件．
表示两条直线，求实数
的值．
，
，
，
四点共线，求直线方程
．
与点
，过点
作直线
交抛物线于
两点，求线段
中点
的轨迹方程．
，如图所示表示平行于对称轴
（即
轴）的光线在抛物线上的点
的反射情况，设
纵坐标为
，
取何值时，从入射点
的光线路程
最短．
推荐套卷
甲、乙两人共同抛掷一枚硬币，规定硬币正面朝上甲得1分，否则乙得1分，先积得3分者获胜，并结束游戏．
（Ⅰ）求在前3次抛掷中甲得2分，乙得1分的概率；
（Ⅱ）若甲已经积得2分，乙已经积得1分，求甲最终获胜的概率；
（Ⅲ）用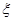表示决出胜负抛硬币的次数，求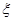的分布列及数学期望．
粤公网安备 44130202000953号