已知函数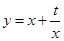 有如下性质:如果常数
有如下性质:如果常数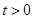 ,那么该函数在
,那么该函数在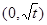 上是减函数,在
上是减函数,在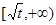 上是增函数.
上是增函数.
(1)已知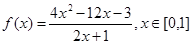 ,利用上述性质,求函数
,利用上述性质,求函数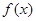 的单调区间和值域;
的单调区间和值域;
(2)对于(1)中的函数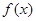 和函数
和函数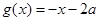 ,若对任意
,若对任意 ∈[0,1],总存在
∈[0,1],总存在 ∈[0,1],使得
∈[0,1],使得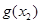 =
=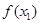 成立,求实数
成立,求实数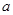 的值.
的值.
推荐套卷
已知函数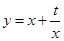 有如下性质:如果常数
有如下性质:如果常数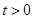 ,那么该函数在
,那么该函数在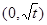 上是减函数,在
上是减函数,在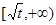 上是增函数.
上是增函数.
(1)已知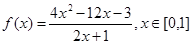 ,利用上述性质,求函数
,利用上述性质,求函数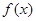 的单调区间和值域;
的单调区间和值域;
(2)对于(1)中的函数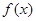 和函数
和函数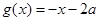 ,若对任意
,若对任意 ∈[0,1],总存在
∈[0,1],总存在 ∈[0,1],使得
∈[0,1],使得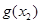 =
=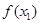 成立,求实数
成立,求实数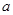 的值.
的值.