如图，BC是⊙O的直径，点A在⊙O上，AD⊥BC，垂足为D，弧AE=弧 AB，BE分别交AD、AC于点F、G．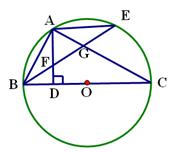
（1）判断△FAG的形状，并说明理由；
（2）若点E和点A在BC的两侧，BE、AC的延长线交于点G，AD的延长线交BE于点F，其余条件不变，（1）中的结论还成立吗？请说明理由．
相关试题
和点
在抛物线
上. 
的值及点
的坐标；
在
轴上，且满足△
是以
为直角边的直角三角形，求点
，点B的对应点为
. 点M（2,0）在x轴上，当抛物线向右平移到某个位置时，
最短，求此时抛物线的函数解析式.相关知识点
推荐套卷
如图，BC是⊙O的直径，点A在⊙O上，AD⊥BC，垂足为D，弧AE=弧 AB，BE分别交AD、AC于点F、G．
（1）判断△FAG的形状，并说明理由；
（2）若点E和点A在BC的两侧，BE、AC的延长线交于点G，AD的延长线交BE于点F，其余条件不变，（1）中的结论还成立吗？请说明理由．
粤公网安备 44130202000953号