已知Rt△ABC中,AC=BC,∠C=90°,D为AB边的中点,∠EDF=90°,如图①∠EDF的两边分别交AC、CB(或它们的延长线)于E、F.当∠EDF的边DE⊥AC于E时, ,
, ,
, 满足
满足 ;
;
(1)如图②,当∠EDF的边DE和AC不垂直时,请证明上述结论仍然成立;
(2)如图③,当∠EDF的边DE与AC的延长线交于点E的情况下,上述结论是否成立?若成立,请给予证明;若不成立, ,
, ,
, 又有怎样的数量关系?请写出你的猜想,不需证明.
又有怎样的数量关系?请写出你的猜想,不需证明.
相关知识点
推荐套卷
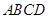 的周长为52cm,对角线
的周长为52cm,对角线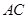 、
、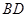 交于点
交于点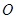 ,且
,且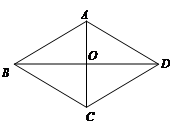
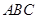 的顶点都在格点上,且△
的顶点都在格点上,且△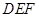 关于点
关于点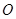 成中心对称.
成中心对称.
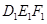 .
.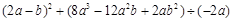 ,其中
,其中 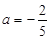 ,
,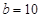 .
.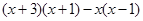 .
. .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号