小红将笔记本电脑水平放置在桌子上,显示屏OB与底板OA所在水平线的夹角为120°时,感觉最舒适(如图1),侧面示意图为图2;使用时为了散热,她在底板下面垫入散热架ACO'后,电脑转到AO'B'位置(如图3),侧面示意图为图4.已知OA=OB=24cm,O'C⊥OA于点C,O'C=12cm.
(1)求∠CAO'的度数.
(2)显示屏的顶部B'比原来升高了多少?
(3)如图4,垫入散热架后,要使显示屏O'B'与水平线的夹角仍保持120°,则显示屏O'B'应绕点O'按顺时针方向旋转多少度?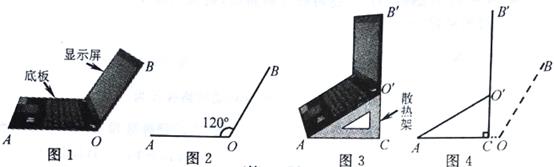
相关知识点
推荐套卷
 满足条件
满足条件 时,求出方程
时,求出方程 的根
的根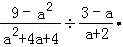
 ,其中
,其中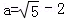 .
. )上,再按顺时针方向绕点B翻转到△
)上,再按顺时针方向绕点B翻转到△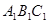 的位置(
的位置( 在
在 的位置,其平移的距离为线段AC的长度(此时
的位置,其平移的距离为线段AC的长度(此时 恰好靠在墙边)。
恰好靠在墙边)。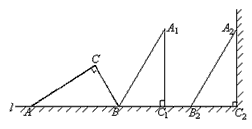
 粤公网安备 44130202000953号
粤公网安备 44130202000953号