如图,在一个横截面为Rt△ABC的物体中,∠ACB=90°,∠CAB=30°,BC=1米。工人师傅把此物体搬到墙边,先将AB边放在地面(直线 )上,再按顺时针方向绕点B翻转到△
)上,再按顺时针方向绕点B翻转到△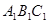 的位置(
的位置( 在
在 上),最后沿
上),最后沿 的方向平移到△
的方向平移到△ 的位置,其平移的距离为线段AC的长度(此时
的位置,其平移的距离为线段AC的长度(此时 恰好靠在墙边)。
恰好靠在墙边)。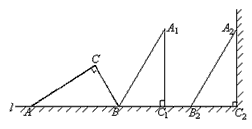
(1)求出AB的长;
(2)求出AC的长;
(3)画出在搬动此物的整个过程A点所经过的路径,并求出该路径的长度(精确到0.1米)。
推荐套卷
如图,在一个横截面为Rt△ABC的物体中,∠ACB=90°,∠CAB=30°,BC=1米。工人师傅把此物体搬到墙边,先将AB边放在地面(直线 )上,再按顺时针方向绕点B翻转到△
)上,再按顺时针方向绕点B翻转到△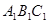 的位置(
的位置( 在
在 上),最后沿
上),最后沿 的方向平移到△
的方向平移到△ 的位置,其平移的距离为线段AC的长度(此时
的位置,其平移的距离为线段AC的长度(此时 恰好靠在墙边)。
恰好靠在墙边)。
(1)求出AB的长;
(2)求出AC的长;
(3)画出在搬动此物的整个过程A点所经过的路径,并求出该路径的长度(精确到0.1米)。