如图,抛物线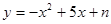 经过点A(1,0),与y轴交于点B.
经过点A(1,0),与y轴交于点B.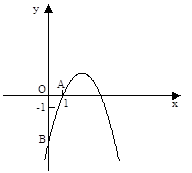
(1)求抛物线的解析式;
(2)P是y轴上一点,且△PAB是以AB为腰的等腰三角形,试求P点坐标.将抛物线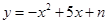 沿着坐标轴方向经过怎样的一次平移可以使它使它经过原点.
沿着坐标轴方向经过怎样的一次平移可以使它使它经过原点.
相关知识点
推荐套卷
如图,抛物线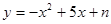 经过点A(1,0),与y轴交于点B.
经过点A(1,0),与y轴交于点B.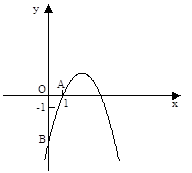
(1)求抛物线的解析式;
(2)P是y轴上一点,且△PAB是以AB为腰的等腰三角形,试求P点坐标.将抛物线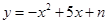 沿着坐标轴方向经过怎样的一次平移可以使它使它经过原点.
沿着坐标轴方向经过怎样的一次平移可以使它使它经过原点.