已知圆
的圆心在
轴上，半径为2，直线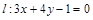
被圆截得的弦长为
，且圆心在直线
的上方．
（1）求圆的方程；
（2）设
，
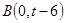（2≤t≤4），若圆是
的内切圆，求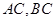
边所在直线的斜率（用
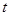表示）
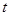（3）在（2）的条件下求的面积S的最大值及对应的值．
相关试题
相关知识点
推荐套卷
已知圆的圆心在轴上，半径为2，直线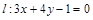被圆截得的弦长为，且圆心在直线的上方．
（1）求圆的方程；
（2）设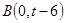，（2≤t≤4），若圆是的内切圆，求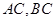边所在直线的斜率（用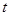表示）
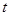（3）在（2）的条件下求的面积S的最大值及对应的值．
粤公网安备 44130202000953号