2014年11月10日APEC会议在北京召开,某服务部需从大学生中招收志愿者,被招收的志愿者需参加笔试和面试两部分,把参加笔试的60名大学生按成绩分组:第1组[75,80)有3人,第2组[80,85)有21人,第3组[85,90)有18人,第4组[90,95)有12人,第5组[95,100)有6人
(1)现决定在笔试成绩较高的第3、4、5组中用分层抽样抽取12人进行面试,则第3、4、5组各抽取多少人?
(2)已知甲和乙的成绩均在第5组,在(1)的条件下,求甲、乙至少有1人进入面试的概率.
推荐套卷
 BAD=60°.
BAD=60°.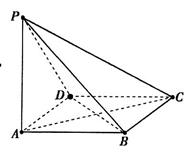
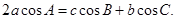
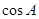 的值;
的值;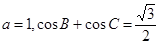 ,求边c的值.
,求边c的值.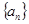 满足
满足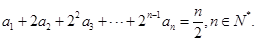
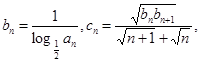 记
记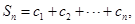 证明:Sn<1.
证明:Sn<1.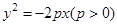 的焦点为
的焦点为 F,过F的直线交y轴正半轴于点,交抛物线于A,B两点,其中A在第二象限。
F,过F的直线交y轴正半轴于点,交抛物线于A,B两点,其中A在第二象限。 ,求
,求 的值.
的值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号