如图,正方形网格中每一个小正方形的边长都为1,每一个小格的顶点叫做格点.以格点为顶点分别按下列要求画三角形: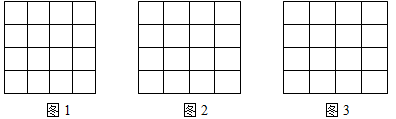
(1)在图1中,画一个三角形,使它的边长都是有理数;
(2)在图2、图3中分别画一个直角三角形,使它们的边长都是无理数,并且要求两个三角形不全等.
相关知识点
推荐套卷
如图,正方形网格中每一个小正方形的边长都为1,每一个小格的顶点叫做格点.以格点为顶点分别按下列要求画三角形:
(1)在图1中,画一个三角形,使它的边长都是有理数;
(2)在图2、图3中分别画一个直角三角形,使它们的边长都是无理数,并且要求两个三角形不全等.