(1)如图1, 是
是 的平分线,请利用该图形画一组以
的平分线,请利用该图形画一组以 所在直线为对称轴且一条边在OP上的全等三角形,并用符号表示出来;
所在直线为对称轴且一条边在OP上的全等三角形,并用符号表示出来;
(2)请你参考这个作全等三角形的方法,解答下列问题:
①如图2:在 中,
中, °,
°,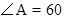 °,
°, 平分
平分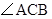 ,试判断
,试判断 和
和 、
、 之间的数量关系;
之间的数量关系;
②如图3,在四边形 中,
中, 平分
平分 ,
, ,
, ,
, ,求
,求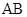 的长.
的长.
相关知识点
推荐套卷
(1)如图1, 是
是 的平分线,请利用该图形画一组以
的平分线,请利用该图形画一组以 所在直线为对称轴且一条边在OP上的全等三角形,并用符号表示出来;
所在直线为对称轴且一条边在OP上的全等三角形,并用符号表示出来;
(2)请你参考这个作全等三角形的方法,解答下列问题:
①如图2:在 中,
中, °,
°,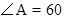 °,
°, 平分
平分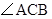 ,试判断
,试判断 和
和 、
、 之间的数量关系;
之间的数量关系;
②如图3,在四边形 中,
中, 平分
平分 ,
, ,
, ,
, ,求
,求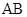 的长.
的长.