直角坐标系中,已知A(1,0),以点A为圆心画圆,点M(4,4)在⊙A上,直线y=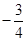 x+b过点M,分别交x轴、y轴于B、C两点.
x+b过点M,分别交x轴、y轴于B、C两点.
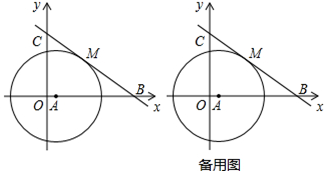
(1)填空:⊙A的半径为 ,b= .(不需写解答过程)
(2)判断直线BC与⊙A的位置关系,并说明理由.
(3)点D是线段OC上的一点,连接MA、MD并延长交⊙A于E、F,若AE⊥AF,求点D的坐标.
相关知识点
推荐套卷
直角坐标系中,已知A(1,0),以点A为圆心画圆,点M(4,4)在⊙A上,直线y=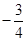 x+b过点M,分别交x轴、y轴于B、C两点.
x+b过点M,分别交x轴、y轴于B、C两点.

(1)填空:⊙A的半径为 ,b= .(不需写解答过程)
(2)判断直线BC与⊙A的位置关系,并说明理由.
(3)点D是线段OC上的一点,连接MA、MD并延长交⊙A于E、F,若AE⊥AF,求点D的坐标.