已知 为实数,用[
为实数,用[ ]表示不超过
]表示不超过 的最大整数,例如
的最大整数,例如 ,
, ,
, .对于函数
.对于函数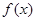 ,若存在
,若存在 且
且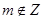 ,使得
,使得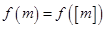 ,则称函数
,则称函数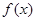 是
是 函数.
函数.
(Ⅰ)判断函数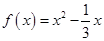 ,
, 是否是
是否是 函数;(只需写出结论)
函数;(只需写出结论)
(Ⅱ)已知 ,请写出
,请写出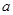 的一个值,使得
的一个值,使得 为
为 函数,并给出证明;
函数,并给出证明;
(Ⅲ)设函数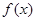 是定义在
是定义在 上的周期函数,其最小周期为
上的周期函数,其最小周期为 .若
.若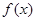 不是
不是 函数,求
函数,求 的最小值.
的最小值.
推荐套卷
已知 为实数,用[
为实数,用[ ]表示不超过
]表示不超过 的最大整数,例如
的最大整数,例如 ,
, ,
, .对于函数
.对于函数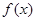 ,若存在
,若存在 且
且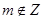 ,使得
,使得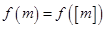 ,则称函数
,则称函数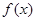 是
是 函数.
函数.
(Ⅰ)判断函数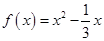 ,
, 是否是
是否是 函数;(只需写出结论)
函数;(只需写出结论)
(Ⅱ)已知 ,请写出
,请写出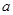 的一个值,使得
的一个值,使得 为
为 函数,并给出证明;
函数,并给出证明;
(Ⅲ)设函数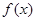 是定义在
是定义在 上的周期函数,其最小周期为
上的周期函数,其最小周期为 .若
.若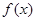 不是
不是 函数,求
函数,求 的最小值.
的最小值.