已知椭圆
的离心率为
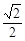，左、右焦点分别为E、F，椭圆上的点P满足
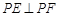，且△PEF的面积为1，抛物线
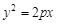经过点（2，2）．
（Ⅰ）分别求椭圆与抛物线的方程；
（Ⅱ）已知
为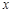
轴上一点，倾斜角为
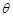的直线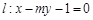
交椭圆于A、B两点，线段AB的中点为M，直线QM交抛物线于C、D两点，四边形ACBD的面积记为S，若对任意直线l，都存在点Q，使得
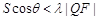，求实数
的取值范围．
相关试题
的方程为
，圆
的方程为
．
，其中
且m为常数．
时函数
在区间
上的单调性，并证明； 
在
处取得极值，求
的值，并讨论函数
．
的递减区间；
上的最值．
满足到定点
的距离与到定点
距离之比为
．
的方程；
的直线
与曲线
，若
，求直线
中，
，
，
为正三角形，且平面
平面
．
；
的余弦值．推荐套卷
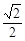已知椭圆的离心率为，左、右焦点分别为E、F，椭圆上的点P满足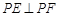，且△PEF的面积为1，抛物线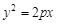经过点（2，2）．
（Ⅰ）分别求椭圆与抛物线的方程；
（Ⅱ）已知为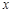轴上一点，倾斜角为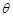的直线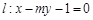交椭圆于A、B两点，线段AB的中点为M，直线QM交抛物线于C、D两点，四边形ACBD的面积记为S，若对任意直线l，都存在点Q，使得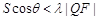，求实数的取值范围．
粤公网安备 44130202000953号