如图,长方形纸片ABCD,AD∥BC,将长方形纸片折叠,使点D与点B重合,点C落在点C'处,折痕为EF,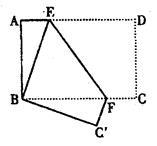
(1)求证:BE=BF.
(2)若∠ABE=18°,求∠BFE的度数.
(3)若AB=6,AD=8,求AE的长.
相关知识点
推荐套卷
如图,长方形纸片ABCD,AD∥BC,将长方形纸片折叠,使点D与点B重合,点C落在点C'处,折痕为EF,
(1)求证:BE=BF.
(2)若∠ABE=18°,求∠BFE的度数.
(3)若AB=6,AD=8,求AE的长.