如图，在一个长AB=40m、宽BC=30m的长方形小操场上，王刚从A点出发，沿着A→B→C的路线以3m/s的速度跑向C地．当他出发4s后，张华有东西需要交给他，就从A地出发沿王刚走的路线追赶，当张华跑到距B地8m的D处时，他和王刚在阳光下的影子恰好重叠在同一条直线上．此时，A处一根电线杆在阳光下的影子也恰好落在对角线AC上．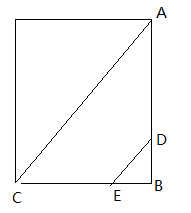
（1）求他们的影子重叠时，两人相距多少米（DE的长）？
（2）求张华追赶王刚的速度是多少？
，如3※2=
．那么12※4=" _______________" 。
与正比例函数
的图象有一个交点是（
，
），则它们的另一个交点的坐标是_______________．相关知识点
推荐套卷
如图，在一个长AB=40m、宽BC=30m的长方形小操场上，王刚从A点出发，沿着A→B→C的路线以3m/s的速度跑向C地．当他出发4s后，张华有东西需要交给他，就从A地出发沿王刚走的路线追赶，当张华跑到距B地8m的D处时，他和王刚在阳光下的影子恰好重叠在同一条直线上．此时，A处一根电线杆在阳光下的影子也恰好落在对角线AC上．
（1）求他们的影子重叠时，两人相距多少米（DE的长）？
（2）求张华追赶王刚的速度是多少？
粤公网安备 44130202000953号