以原点O为圆心,1cm为半径的圆分别交 、
、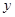 轴的正半轴于A、B两点,点P的坐标为(2,0),动点Q从点B处出发,沿圆周按顺时针方向匀速运动一周,设运动的时间为秒.
轴的正半轴于A、B两点,点P的坐标为(2,0),动点Q从点B处出发,沿圆周按顺时针方向匀速运动一周,设运动的时间为秒.
(1)如图一,当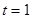 时,直线PQ恰好与⊙O第一次相切,连接OQ.求此时点Q的运动速度(结果保留
时,直线PQ恰好与⊙O第一次相切,连接OQ.求此时点Q的运动速度(结果保留 );
);
(2)若点Q按照(1)中的速度继续运动.
①当为何值时,以O、P、Q为顶点的三角形是直角三角形;
②在①的条件下,如果直线PQ与⊙O相交,请求出直线PQ被⊙O所截的弦长.
相关知识点
推荐套卷
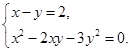
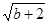 =0,求方程
=0,求方程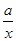 +bx=1的解.
+bx=1的解. 粤公网安备 44130202000953号
粤公网安备 44130202000953号