在一个六角形体育馆的一角MAN内，用长为a的围栏设置一个运动器材存储区域（如图所示），已知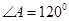
，B是墙角线AM上的一点，C是墙角线AN上的一点．
（1）若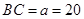
，求存储区域面积的最大值；
（2）若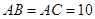
，在折线MBCN内选一点D，使
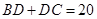，求四边形存储区域DBAC的最大面积．
的前
项和为
，且
和
.
,求
的前
；
，
都成立，求整数
的最大值.
是等差数列，且
.
，求数列
的前
项和．
中，角
的对边分别为
且
.
;
，求
的前
项和
,又
，求数列
的前
.
中，
分别为角
的对边，
.
的度数；
,求
与
的值.推荐套卷
在一个六角形体育馆的一角MAN内，用长为a的围栏设置一个运动器材存储区域（如图所示），已知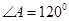，B是墙角线AM上的一点，C是墙角线AN上的一点．
（1）若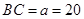，求存储区域面积的最大值；
（2）若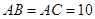，在折线MBCN内选一点D，使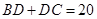，求四边形存储区域DBAC的最大面积．
粤公网安备 44130202000953号