某厂生产一种产品,每件产品的成本为40元,出厂单价定为60元,该厂为鼓励销售商订购,决定当一次订购量超过100件时,每多订购一件,订购的全部产品的出场单价就降低0.02元,根据市场调查,销售商一次订购量不会超过600件.
(1)设一次订购x件,产品的实际出厂单价p元,写出函数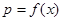 的表达式;
的表达式;
(2)当销售商一次订购多少件产品时,该厂获得的利润最大?其最大利润是多少?
推荐套卷
某厂生产一种产品,每件产品的成本为40元,出厂单价定为60元,该厂为鼓励销售商订购,决定当一次订购量超过100件时,每多订购一件,订购的全部产品的出场单价就降低0.02元,根据市场调查,销售商一次订购量不会超过600件.
(1)设一次订购x件,产品的实际出厂单价p元,写出函数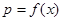 的表达式;
的表达式;
(2)当销售商一次订购多少件产品时,该厂获得的利润最大?其最大利润是多少?