如图,在菱形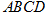 中,对角线
中,对角线 与
与 相交于点
相交于点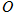 ,
, ,在菱形
,在菱形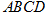 的外部以
的外部以 为边作等边三角形
为边作等边三角形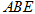 。点
。点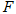 是对角线
是对角线 上一动点(点
上一动点(点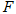 不与点
不与点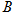 、D重合),将线段
、D重合),将线段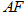 绕点
绕点 顺时针方向旋转
顺时针方向旋转 得到线段
得到线段 ,连接
,连接 。
。
(1)求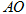 的长;
的长;
(2)如图2,当点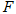 在线段
在线段 上,且点
上,且点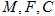 三点在同一条直线上时,求证:
三点在同一条直线上时,求证: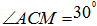
(3)连接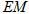 ,若
,若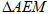 的面积为40,请画出图形,并直接写出
的面积为40,请画出图形,并直接写出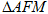 的周长。
的周长。
相关知识点
推荐套卷
如图,在菱形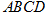 中,对角线
中,对角线 与
与 相交于点
相交于点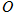 ,
, ,在菱形
,在菱形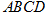 的外部以
的外部以 为边作等边三角形
为边作等边三角形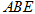 。点
。点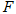 是对角线
是对角线 上一动点(点
上一动点(点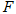 不与点
不与点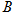 、D重合),将线段
、D重合),将线段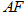 绕点
绕点 顺时针方向旋转
顺时针方向旋转 得到线段
得到线段 ,连接
,连接 。
。
(1)求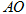 的长;
的长;
(2)如图2,当点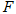 在线段
在线段 上,且点
上,且点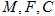 三点在同一条直线上时,求证:
三点在同一条直线上时,求证: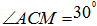
(3)连接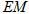 ,若
,若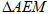 的面积为40,请画出图形,并直接写出
的面积为40,请画出图形,并直接写出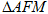 的周长。
的周长。