点 到
到 的距离是点
的距离是点 到
到 的距离的
的距离的 倍.
倍.
(1)求点 的轨迹方程;
的轨迹方程;
(2)点 与点
与点 关于点
关于点 对称,点
对称,点 ,求
,求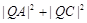 的最大值和最小值.
的最大值和最小值.
(3)若过 的直线从左向右依次交第(2)问中
的直线从左向右依次交第(2)问中 的轨迹于不同两点
的轨迹于不同两点 ,
, ,
,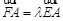 ,判断
,判断 的取值范围并证明.
的取值范围并证明.
推荐套卷
点 到
到 的距离是点
的距离是点 到
到 的距离的
的距离的 倍.
倍.
(1)求点 的轨迹方程;
的轨迹方程;
(2)点 与点
与点 关于点
关于点 对称,点
对称,点 ,求
,求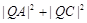 的最大值和最小值.
的最大值和最小值.
(3)若过 的直线从左向右依次交第(2)问中
的直线从左向右依次交第(2)问中 的轨迹于不同两点
的轨迹于不同两点 ,
, ,
,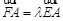 ,判断
,判断 的取值范围并证明.
的取值范围并证明.