如图所示,已知BD为△ABC的角平分线,CD为△ABC外角∠ACE的平分线,且与BD交于点D;
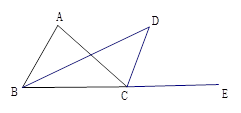
(1)若∠ABC=60°,∠DCE=70°,则∠D= °;
(2)若∠ABC=70°,∠A=80°,则∠D= °;
(3)当∠ABC和∠ACB在变化,而∠A始终保持不变,则∠D是否发生变化?为什么?由此你能得出什么结论?(用含∠A的式子表示∠D)
相关知识点
推荐套卷
如图所示,已知BD为△ABC的角平分线,CD为△ABC外角∠ACE的平分线,且与BD交于点D;

(1)若∠ABC=60°,∠DCE=70°,则∠D= °;
(2)若∠ABC=70°,∠A=80°,则∠D= °;
(3)当∠ABC和∠ACB在变化,而∠A始终保持不变,则∠D是否发生变化?为什么?由此你能得出什么结论?(用含∠A的式子表示∠D)