如图,已知△ABC中,∠B="90" º,AB=16cm,BC=12cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.
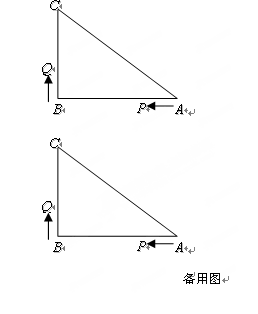
(1)出发2秒后,求PQ的长;
(2)当点Q在边BC上运动时,出发几秒钟后,△PQB能形成等腰三角形?
(3)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.
相关知识点
推荐套卷
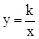 (x > 0,k是常数)的图象经过点A(1,4),点B(m , n),其中m>1, AM⊥x轴,垂足为M,BN⊥y轴,垂足为N,AM与BN的交点为C.
(x > 0,k是常数)的图象经过点A(1,4),点B(m , n),其中m>1, AM⊥x轴,垂足为M,BN⊥y轴,垂足为N,AM与BN的交点为C.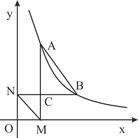
 粤公网安备 44130202000953号
粤公网安备 44130202000953号