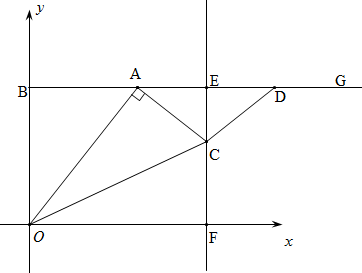
（钦州）如图，在平面直角坐标系中，以点B（0，8）为端点的射线BG∥x轴，点A是射线BG上的一个动点（点A与点B不重合）．在射线AG上取AD=OB，作线段AD的垂直平分线，垂足为E，且与x轴交于点F，过点A作AC⊥OA，交射线EF于点C．连接OC、CD，设点A的横坐标为t．
（1）用含t的式子表示点E的坐标为_______；
（2）当t为何值时，∠OCD=180°？
（3）当点C与点F不重合时，设△OCF的面积为S，求S与t之间的函数解析式．