（柳州）如图，已知抛物线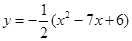
的顶点坐标为M，与x轴相交于A，B两点（点B在点A的右侧），与y轴相交于点C．
（1）用配方法将抛物线的解析式化为顶点式：
（
），并指出顶点M的坐标；
（2）在抛物线的对称轴上找点R，使得CR+AR的值最小，并求出其最小值和点R的坐标；
（3）以AB为直径作⊙N交抛物线于点P（点P在对称轴的左侧），求证：直线MP是⊙N的切线．
相关试题
（柳州）如图，已知抛物线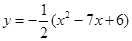的顶点坐标为M，与x轴相交于A，B两点（点B在点A的右侧），与y轴相交于点C．
（1）用配方法将抛物线的解析式化为顶点式：（），并指出顶点M的坐标；
（2）在抛物线的对称轴上找点R，使得CR+AR的值最小，并求出其最小值和点R的坐标；
（3）以AB为直径作⊙N交抛物线于点P（点P在对称轴的左侧），求证：直线MP是⊙N的切线．
0°方向，这时渔船改为向正东方向航行，问渔船有触礁有危险吗？为什么？
粤公网安备 44130202000953号