已知O为坐标原点,抛物线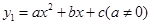 与
与 轴相交于点
轴相交于点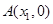 ,
,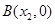 .与
.与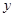 轴交于点C,且O,C两点之间的距离为3,
轴交于点C,且O,C两点之间的距离为3,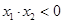 ,
,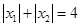 ,点A,C在直线
,点A,C在直线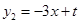 上.
上.
(1)求点C的坐标;
(2)当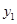 随着
随着 的增大而增大时,求自变量
的增大而增大时,求自变量 的取值范围;
的取值范围;
(3)将抛物线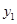 向左平移
向左平移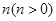 个单位,记平移后
个单位,记平移后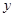 随着
随着 的增大而增大的部分为P,直线
的增大而增大的部分为P,直线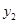 向下平移n个单位,当平移后的直线与P有公共点时,求
向下平移n个单位,当平移后的直线与P有公共点时,求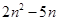 的最小值.
的最小值.
已知O为坐标原点,抛物线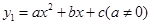 与
与 轴相交于点
轴相交于点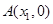 ,
,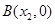 .与
.与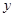 轴交于点C,且O,C两点之间的距离为3,
轴交于点C,且O,C两点之间的距离为3,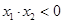 ,
,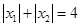 ,点A,C在直线
,点A,C在直线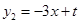 上.
上.
(1)求点C的坐标;
(2)当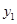 随着
随着 的增大而增大时,求自变量
的增大而增大时,求自变量 的取值范围;
的取值范围;
(3)将抛物线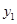 向左平移
向左平移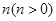 个单位,记平移后
个单位,记平移后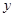 随着
随着 的增大而增大的部分为P,直线
的增大而增大的部分为P,直线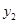 向下平移n个单位,当平移后的直线与P有公共点时,求
向下平移n个单位,当平移后的直线与P有公共点时,求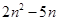 的最小值.
的最小值.