(·湖北鄂州,24题,12分)如图,在平面直角坐标系xoy中,直线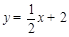 与x 轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是
与x 轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是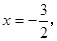 且经过A、C两点,与x轴的另一交点为点B.
且经过A、C两点,与x轴的另一交点为点B.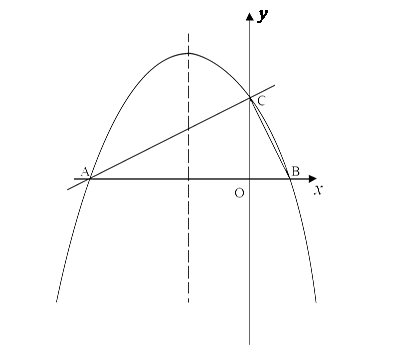
(1)①直接写出点B的坐标;②求抛物线解析式.
(2)若点P为直线AC上方的抛物线上的一点,连接PA,PC.求△PAC的面积的最大值,并求出此时点P的坐标.
(3)抛物线上是否存在点M,过点M作MN垂直x轴于点N,使得以点A、M、N为顶点的三角形与△ABC相似?若存在,求出点M的坐标;若不存在,请说明理由.
(·湖北鄂州,24题,12分)如图,在平面直角坐标系xoy中,直线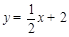 与x 轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是
与x 轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是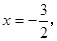 且经过A、C两点,与x轴的另一交点为点B.
且经过A、C两点,与x轴的另一交点为点B.
(1)①直接写出点B的坐标;②求抛物线解析式.
(2)若点P为直线AC上方的抛物线上的一点,连接PA,PC.求△PAC的面积的最大值,并求出此时点P的坐标.
(3)抛物线上是否存在点M,过点M作MN垂直x轴于点N,使得以点A、M、N为顶点的三角形与△ABC相似?若存在,求出点M的坐标;若不存在,请说明理由.