（·湖南益阳）已知点P是线段AB上与点A不重合的一点，且AP＜PB．AP绕点A逆时针旋转角α（0°＜α≤90°）得到AP1，BP绕点B顺时针也旋转角α得到BP2，连接PP1、PP2．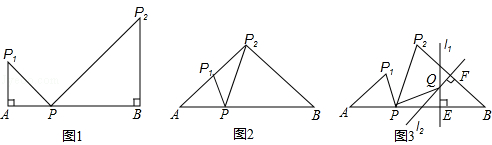
（1）如图1，当α=90°时，求∠P1PP2的度数；
（2）如图2，当点P2在AP1的延长线上时，求证：△P2P1P∽△P2PA；
（3）如图3，过BP的中点E作l1⊥BP，过BP2的中点F作l2⊥BP2，l1与l2交于点Q，连接PQ，求证：P1P⊥PQ．
相关试题
是⊙
的直径，AC与⊙
.
∥
；
，
，求线段CE的长．
如图6，小明以3米/秒的速度从山脚A点爬到山顶B点，已知点B到山脚的垂直距离
为24米，且山坡坡角
的度数为
，问小明从山脚爬上山顶需要多少时间？（结果精确到
）（参考数据：
，
，
）
，其中
.△ABC在方格纸中的位置如图5所示，方格纸中的每个小正方形的边长为1个单位.
（1）△
与△ABC关于纵轴（
轴）对称，请你在图5中画出△；
（2）将△ABC向下平移8个单位后得到△
，请你在图5中画出△.
.
粤公网安备 44130202000953号