(·湖北衡阳,23题,分)(本小题满分6分)如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(3,2)B(3,5)C(1,2).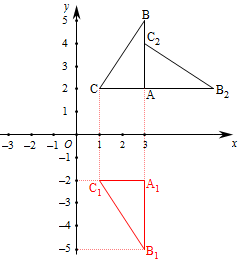
(1)在平面直角坐标系中画出△ABC关于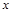 轴对称的△A1B1C1;
轴对称的△A1B1C1;
(2)把△ABC绕点A顺时针旋转一定的角度,得图中的△AB2C2,点C2在AB上.
①旋转角为多少度?
②写出点B2的坐标.
(·湖北衡阳,23题,分)(本小题满分6分)如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(3,2)B(3,5)C(1,2).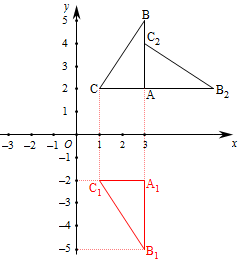
(1)在平面直角坐标系中画出△ABC关于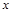 轴对称的△A1B1C1;
轴对称的△A1B1C1;
(2)把△ABC绕点A顺时针旋转一定的角度,得图中的△AB2C2,点C2在AB上.
①旋转角为多少度?
②写出点B2的坐标.