(遂宁)如图,已知抛物线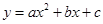 经过A(﹣2,0),B(4,0),C(0,3)三点.
经过A(﹣2,0),B(4,0),C(0,3)三点.
(1)求该抛物线的解析式;
(2)在y轴上是否存在点M,使△ACM为等腰三角形?若存在,请直接写出所有满足要求的点M的坐标;若不存在,请说明理由;
(3)若点P(t,0)为线段AB上一动点(不与A,B重合),过P作y轴的平行线,记该直线右侧与△ABC围成的图形面积为S,试确定S与t的函数关系式.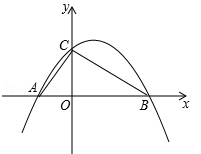
(遂宁)如图,已知抛物线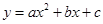 经过A(﹣2,0),B(4,0),C(0,3)三点.
经过A(﹣2,0),B(4,0),C(0,3)三点.
(1)求该抛物线的解析式;
(2)在y轴上是否存在点M,使△ACM为等腰三角形?若存在,请直接写出所有满足要求的点M的坐标;若不存在,请说明理由;
(3)若点P(t,0)为线段AB上一动点(不与A,B重合),过P作y轴的平行线,记该直线右侧与△ABC围成的图形面积为S,试确定S与t的函数关系式.