(攀枝花)如图,已知抛物线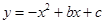 与x轴交于A(﹣1,0)、B(3,0)两点,与y轴交于点C,抛物线的对称轴与抛物线交于点P、与直线BC相交于点M,连接PB.
与x轴交于A(﹣1,0)、B(3,0)两点,与y轴交于点C,抛物线的对称轴与抛物线交于点P、与直线BC相交于点M,连接PB.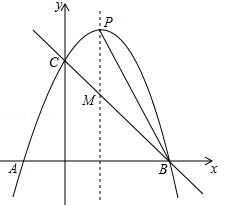
(1)求该抛物线的解析式;
(2)在(1)中位于第一象限内的抛物线上是否存在点D,使得△BCD的面积最大?若存在,求出D点坐标及△BCD面积的最大值;若不存在,请说明理由.
(3)在(1)中的抛物线上是否存在点Q,使得△QMB与△PMB的面积相等?若存在,求出点Q的坐标;若不存在,请说明理由.
(攀枝花)如图,已知抛物线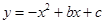 与x轴交于A(﹣1,0)、B(3,0)两点,与y轴交于点C,抛物线的对称轴与抛物线交于点P、与直线BC相交于点M,连接PB.
与x轴交于A(﹣1,0)、B(3,0)两点,与y轴交于点C,抛物线的对称轴与抛物线交于点P、与直线BC相交于点M,连接PB.
(1)求该抛物线的解析式;
(2)在(1)中位于第一象限内的抛物线上是否存在点D,使得△BCD的面积最大?若存在,求出D点坐标及△BCD面积的最大值;若不存在,请说明理由.
(3)在(1)中的抛物线上是否存在点Q,使得△QMB与△PMB的面积相等?若存在,求出点Q的坐标;若不存在,请说明理由.