（广元）如图，已知抛物线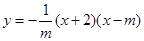
（
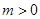）与x轴相交干点A、B．与y轴相交于点C，且点A在点B的左侧．
（1）若抛物经过点C（2，2），求实数m的值；
（2）在（1）的条件下，解答下列问题：
①求出△ABC的面积；
②在抛物线的对称轴上找一点H，使AH+CH最小，并求出点H的坐标；
（3）在第四象限内，抛物线上是否存在点M，使得以点A、B、M为顶点的三角形与△ACB相似？若存在，求m的值；若不存在．请说明理由．
（广元）如图，已知抛物线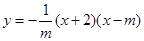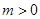（）与x轴相交干点A、B．与y轴相交于点C，且点A在点B的左侧．
（1）若抛物经过点C（2，2），求实数m的值；
（2）在（1）的条件下，解答下列问题：
①求出△ABC的面积；
②在抛物线的对称轴上找一点H，使AH+CH最小，并求出点H的坐标；
（3）在第四象限内，抛物线上是否存在点M，使得以点A、B、M为顶点的三角形与△ACB相似？若存在，求m的值；若不存在．请说明理由．
的值．
＝
(1－
)；
＝
)；
＝
)；…
＋
＋
＝
.
粤公网安备 44130202000953号