已知,AB是⊙O的直径,AB=8,点C在⊙O的半径OA上运动,PC⊥AB,垂足为C,PC=5,PT为⊙O的切线,切点为T.
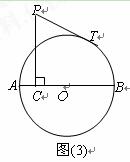
⑴如图⑴,当C点运动到O点时,求PT的长;
⑵如图⑵,当C点运动 到A点时,连结PO、BT,求证:PO∥BT;
到A点时,连结PO、BT,求证:PO∥BT;
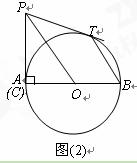
⑶如图⑶,设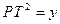 ,
,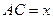 ,求
,求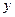 与
与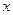 的函数关系式及
的函数关系式及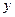 的
的 最小值.
最小值.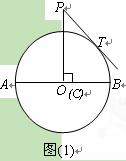
相关知识点
推荐套卷
已知,AB是⊙O的直径,AB=8,点C在⊙O的半径OA上运动,PC⊥AB,垂足为C,PC=5,PT为⊙O的切线,切点为T.
⑴如图⑴,当C点运动到O点时,求PT的长;
⑵如图⑵,当C点运动 到A点时,连结PO、BT,求证:PO∥BT;
到A点时,连结PO、BT,求证:PO∥BT;
⑶如图⑶,设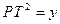 ,
,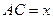 ,求
,求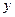 与
与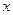 的函数关系式及
的函数关系式及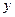 的
的 最小值.
最小值.

