如图,隧道的截面由抛物线 和矩形
和矩形 构成,矩形的长
构成,矩形的长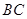 为
为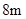 ,宽
,宽 为
为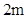 ,以
,以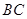 所在的直线为
所在的直线为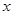 轴,线段
轴,线段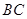 的中垂线为
的中垂线为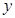 轴,建立平面直角坐标系,
轴,建立平面直角坐标系,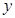 轴是抛物线的对称轴,顶点
轴是抛物线的对称轴,顶点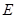 到坐标原点
到坐标原点 的距离为
的距离为 .
.
(1)求抛物线的解析式; (2)一辆货运卡车高
(2)一辆货运卡车高 ,宽2.4m,它能通过该隧道吗?
,宽2.4m,它能通过该隧道吗?
(3)如果该隧道内设双行道,为了安全起见,在隧道正中间设
有0.4m的隔离带,则该辆货运卡车还能通过隧道吗?
相关知识点
推荐套卷
如图,隧道的截面由抛物线 和矩形
和矩形 构成,矩形的长
构成,矩形的长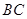 为
为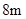 ,宽
,宽 为
为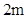 ,以
,以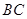 所在的直线为
所在的直线为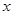 轴,线段
轴,线段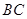 的中垂线为
的中垂线为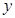 轴,建立平面直角坐标系,
轴,建立平面直角坐标系,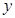 轴是抛物线的对称轴,顶点
轴是抛物线的对称轴,顶点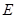 到坐标原点
到坐标原点 的距离为
的距离为 .
.
(1)求抛物线的解析式; (2)一辆货运卡车高
(2)一辆货运卡车高 ,宽2.4m,它能通过该隧道吗?
,宽2.4m,它能通过该隧道吗?
(3)如果该隧道内设双行道,为了安全起见,在隧道正中间设
有0.4m的隔离带,则该辆货运卡车还能通过隧道吗?