(内江)(1)填空: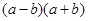 = ;
= ;
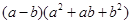 = ;
= ;
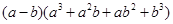 = .
= .
(2)猜想: = (其中n为正整数,且
= (其中n为正整数,且 ).
).
(3)利用(2)猜想的结论计算: .
.
(内江)(1)填空: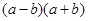 = ;
= ;
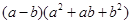 = ;
= ;
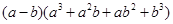 = .
= .
(2)猜想: = (其中n为正整数,且
= (其中n为正整数,且 ).
).
(3)利用(2)猜想的结论计算: .
.