【问题提出】
如图①,已知⊿ABC是等边三角形,点E在线段AB上,点D在直线BC上,且DE=EC,将⊿BCE绕点C顺时针旋转 至⊿ACF,连接EF。
至⊿ACF,连接EF。
试证明:AB=DB+AF。
【类比探究】
(1)如图②,如果点E在线段AB的延长线上,其它条件不变,线段AB、DB、AF之间又有怎样的数量关系?请说明理由。
(2)如果点E在线段BA的延长线上,其他条件不变,请在图③的基础上将图形补充完整,并写出AB,DB,AF之间数量关系,不必说明理由。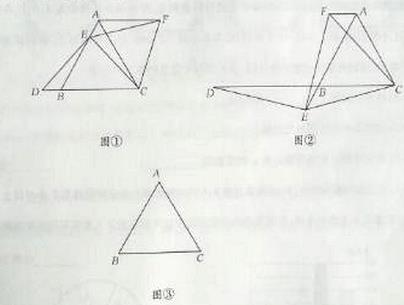
【问题提出】
如图①,已知⊿ABC是等边三角形,点E在线段AB上,点D在直线BC上,且DE=EC,将⊿BCE绕点C顺时针旋转 至⊿ACF,连接EF。
至⊿ACF,连接EF。
试证明:AB=DB+AF。
【类比探究】
(1)如图②,如果点E在线段AB的延长线上,其它条件不变,线段AB、DB、AF之间又有怎样的数量关系?请说明理由。
(2)如果点E在线段BA的延长线上,其他条件不变,请在图③的基础上将图形补充完整,并写出AB,DB,AF之间数量关系,不必说明理由。