（·黑龙江牡丹江）如图，抛物线y=x2+bx+c经过点A（﹣1，0），B（3，0）．请解答下列问题：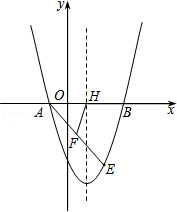
（1）求抛物线的解析式；
（2）点E（2，m）在抛物线上，抛物线的对称轴与x轴交于点H，点F是AE中点，连接FH，求线段FH的长．
注：抛物线y=ax2+bx+c（a≠0）的对称轴是x=﹣
．
相关试题
如图，在△ABC中，∠C＝90°，∠A＝30°．
（1）用尺规作图作AB边上的中垂线DE，交AC于点D，交AB于点E．（保留作图痕迹，不要求写作法和证明）；
（2）连结BD，求证：BD平分∠CBA．
的正整数解．二次函数图象的顶点在原点O，经过点A（1，
）；点F（0，1）在y轴上．直线y=－1与y轴交于点H．
（1）求二次函数的解析式；
（2）点P是（1）中图象上的点，过点P作x轴的垂线与直线y=－1交于点M，求证：FM平分∠OFP；
（3）当△FPM是等边三角形时，求P点的坐标．
如图，在锐角三角形纸片ABC中，AC＞BC，点D，E，F分别在边AB，BC，CA上．
（1）已知：DE∥AC，DF∥BC．
①判断
四边形DECF一定是什么形状？并说明理由．
②裁剪
当AC=24cm，BC=20cm，∠ACB=45°时，请你探索：如何剪四边形DECF，能使它的面积最大，并证明你的结论；
（2）折叠
请你只用两次折叠，确定四边形的顶点D，E，C，F，使它恰好为菱形，并说明你的折法和理由．
粤公网安备 44130202000953号