（·辽宁锦州）如图，在平面直角坐标系中，线段AB的两个端点是A（﹣5，1），B（﹣2，3），线段CD的两个端点是C（﹣5，﹣1），D（﹣2，﹣3）．
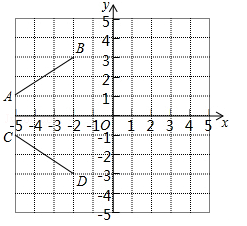
（1）线段AB与线段CD关于直线对称，则对称轴是 ；
（2）平移线段AB得到线段A1B1，若点A的对应点A1的坐标为（1，2），画出平移后的线段A1B1，并写出点B1的坐标为 ．
相关试题
如图，在△ABC中，点D,E,F分别在BC,AB,AC 边上，且DE∥AC，DF∥AB．
（1）如果∠BAC=90°，那么四边形AEDF是形；
（2）如果AD是△ABC的角平分线，那么四边形AEDF是形；
（3）如果∠BAC=90°，AD是△ABC的角平分线，那么四边形AEDF是形，证明你的结论(仅需证明第⑶题结论)．
如图，点C在BD上，在线段BD的同侧作等边△ABC和等边△CDE，AD、BE相交于点F．
（1）求证：BE=AD；
（2）求∠AFB的度数；
（3）设BE与AC交于点M，CE与AD交于点N，连接MN，试判断△MCN的形状，并说明理由．
如图，点E是∠AOB的平分线上一点，EC⊥OA，ED⊥OB，垂足分别是C、D．
求证：（1）∠EDC=∠ECD;
（2）OC=OD;
（3）OE是线段CD的垂直平分线.
粤公网安备 44130202000953号