（·辽宁大连）如图1，在△ABC中，∠C=90°，点D在AC上，且CD>DA，DA=2．点P、Q同时从D点出发，以相同的速度分别沿射线DC、射线DA运动．过点Q作AC的垂线段QR，使QR=PQ，联接PR．当点Q到达A时，点P、Q同时停止运动．设PQ=x．△PQR和△ABC重合部分的面积为S．S关于x的函数图像如图2所示（其中0<x≤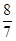
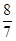，<x≤m时，函数的解析式不同）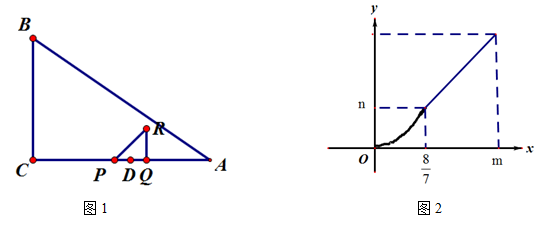
（1）填空：n的值为___________;
（2）求S关于x的函数关系式，并写出x的取值范围．
（·辽宁大连）如图1，在△ABC中，∠C=90°，点D在AC上，且CD>DA，DA=2．点P、Q同时从D点出发，以相同的速度分别沿射线DC、射线DA运动．过点Q作AC的垂线段QR，使QR=PQ，联接PR．当点Q到达A时，点P、Q同时停止运动．设PQ=x．△PQR和△ABC重合部分的面积为S．S关于x的函数图像如图2所示（其中0<x≤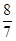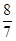，<x≤m时，函数的解析式不同）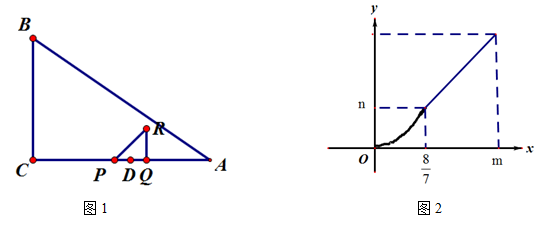
（1）填空：n的值为___________;
（2）求S关于x的函数关系式，并写出x的取值范围．
﹣（3
）﹣4
﹣（﹣8
的和等于﹣1？
﹣（
﹣
）
粤公网安备 44130202000953号