如图,以点P(﹣2,0)为圆心的圆,交x轴于B、C两点(B在C的左侧),交y轴于A、D两点(A在D的下方),AD=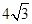 ,将△ABC绕点P旋转180°,得到△MCB.
,将△ABC绕点P旋转180°,得到△MCB.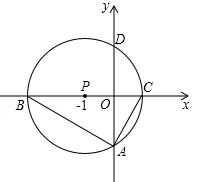
(1)求B、C两点的坐标;
(2)请在图中画出线段MB,MC,并判断四边形ACMB的形状(不必证明),求出点M的坐标.
相关知识点
推荐套卷
如图,以点P(﹣2,0)为圆心的圆,交x轴于B、C两点(B在C的左侧),交y轴于A、D两点(A在D的下方),AD=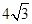 ,将△ABC绕点P旋转180°,得到△MCB.
,将△ABC绕点P旋转180°,得到△MCB.
(1)求B、C两点的坐标;
(2)请在图中画出线段MB,MC,并判断四边形ACMB的形状(不必证明),求出点M的坐标.